Hokama`s Tower Defense (Sem fonte de vida)
No Hokama’s Tower Defense o jogo se dá em um tabuleiro de nxn, o jogador sai do quadrado superior esquerdo na coordenada (0, 0) e precisa chegar no quadrado (n-1, n-1).
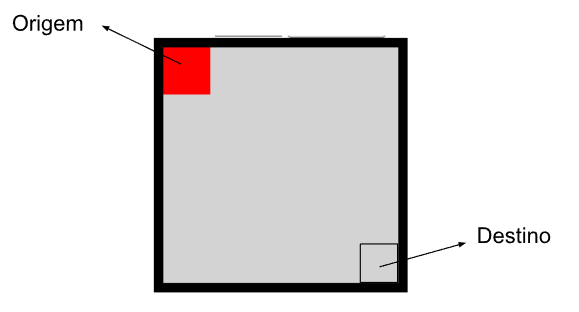
O tabuleiro possui torres de ataque que causam 10 pontos de dano no jogador para cada jogada em que ele esteja em um quadrado adjacente à torre.
No desenho abaixo, o quadrado azul representa uma torre e a área azul claro representa a área de alcance da torre. Note que a torre ataca na diagonal.
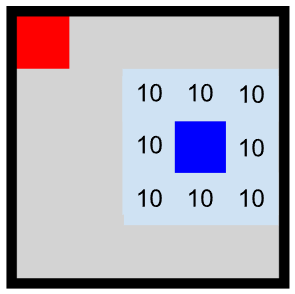
O dano das torres acumula, ou seja, em um quadrado que tiver 3 torres em quadrados adjacentes, caso o jogador passe por ele, sofrerá 30 de dano. O jogador também pode sofrer danos múltiplos de uma mesma torre, caso passe por mais de um quadrado defendido por ela. Na figura a seguir o caminho realizado pelo atacante está marcado em magenta, note que o atacante sofre 50 de dano.
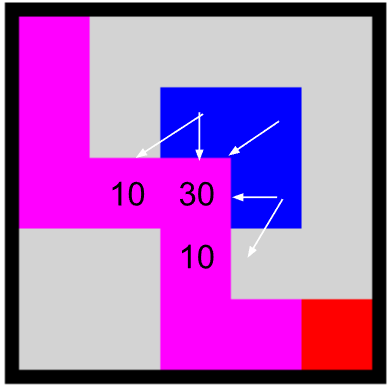
O jogador não pode ocupar o mesmo lugar de uma torre (não pode atravessar uma torre). E você pode supor que em nenhuma das entradas o caminho até o destino está bloqueado, como na figura abaixo.
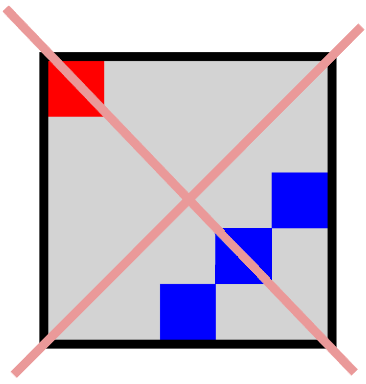
O jogador não pode passar em um lugar repetido!
Para este trabalho você deve fazer um algoritmo exato para encontrar uma solução onde o jogador chega ao seu destino tomando a menor quantidade de dano possível.
Entrada
Como entrada você deve ler um arquivo chamado instXX.in em que a primeira linha indica o tamanho do tabuleiro, e, à partir da segunda linha, um caracter para cada célula do tabuleiro, onde 0 representa um espaço vazio e t uma torre. Como, por exemplo
5 00T00 00TT0 00000 00000 0T000
Um tabuleiro de 5x5 com torres nas posições (2,0), (2,1), (3,1) e (4,1).
Saída
Para saída o seu programa deve escrever um arquivo com as direções que o jogador deve andar para chegar no destino tendo o mínimo de dano possível. Onde S é a jogada de andar para baixo, N andar para cima, L andar para a direita e O andar para a esquerda. O arquivo de soluição deve ter apenas uma linha e todos os caracteres devem estar na mesma linha, e o nome do arquivo da solução da instância instXX.in deve ser solXX.out
Então uma solução ótima da instância acima, tendo -30 de dano pode ser
SSSLLLLS
Avaliação
Seu algoritmo deve rodar qualquer tipo de instância especificada no enunciado, um exemplo de instâncias pode ser encontrado aqui. Outras instâncias maiores serão adicionadas a este conjunto.
No dia da avaliação outras instâncias, de tamanhos variados, não vistas antes, serão apresentadas e seu trabalho terá que solucionar. Sua nota será proporcional à quantidade de instâncias resolvidas de forma ótima.
.